Polyominoes on Thanksgiving

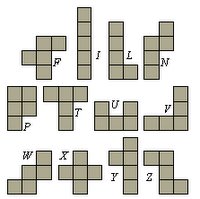
Just before Thanksgiving dinner, a family member was telling me about a children's book that talked about Pentominoes, which I had never heard of before. Apparently they were polygons made up of 5 connected squares, that when combined could form many possible shapes. Given 5 squares, there were 12 possible combinations of shapes that you could form.

I thought about the game Tetris in which you work with similar shapes, but they are made out of 4 squares instead of 5. In Tetris there are 5 possible pieces. This got me thinking: Given n squares, is there some formula, f(n), that would determine how many unique combinations can be formed by connecting the squares?

I took out a napkin and started drawing the possibilities for 0, 1, 2, 3, 4, and 6 squares. 0-4 were easy. For n=6, I drew out over 25 combinations, and then gave up trying to find more:

n --> # of combinations
-----------------------
0 --> 1
1 --> 1
2 --> 1
3 --> 2
4 --> 5
5 --> 12
6 --> 25+

No obvious formulas jumped out at me, so I decided that I should just Google for pentominoes formulas and see if anything came up.

I ended up at Wikipedia where there was an awesome page on Polyominoes, which is apparently the general term for these shapes with a square as the base form. I was amazed at how much analysis existed for Polyominoes. I was even more surprised to find out that no one has yet found the same formula I was looking for. Instead, people have come up with computer algorithms that have empirically counted the combinations.

Just in 2004, someone enumerated the possibilities for up to n=56 which has approximately 6.915 X 10 to the 31 combinations! The results are shown here in the integer sequence A000105 which is maintained by the Online Encyclopedia of Integer Sequences. I didn't even know there was such a thing!. I guess numbers and geometry have always interested me.